- Published on
我的算法日记
- Authors

- Name
- McDaddy(戣蓦)
链表
特点:适合快速插入和删除,不适合快速定位
主要技巧:
dummy虚拟节点
为了防止空指针的出现,比如长度为5的链表要删除倒数第五个节点,那么按理要找到倒数第六个和倒数第四相连,但这时候找倒数第六就会出现空指针异常
反转链表
// 迭代
var reverseList = function (head) {
let prev = null;
let current = head;
while (current) {
const next = current.next;
current.next = prev;
prev = current;
current = next;
}
return prev;
};
// 递归
var reverseList = function (head) {
if (!head || !head.next) {
return head;
}
const last = reverseList(head.next);
head.next.next = head;
head.next = null;
return last;
};
快慢指针(双指针)
应用非常广泛,比如
- 找到链表的中点
- 判断是否有环(如果有环,那么快慢节点迟早相遇)
- 找到倒数第N个节点(快指针先走N步,直到结束,此时慢节点就是倒数第N个节点)
距离相同原理(两个指针走相同的距离相遇)
为什么快慢指针必然会在环中相遇?
- 假设有环的情况,整个环加上开头的部分长度为X + M,第X个点为入环点,环的长度就是M
- 当慢指针走到环末尾时,慢指针走了X + M步,快指针走了2(M + X)步
- 计算快指针在环里走了多少,(2(M + X) - X)/M 就是快指针全路程减去入口的X然后除以环的长度M
- 移项约分后得到结果为
2 + X/M,所以这个值必然是大于2的,快指针在环里走了超过两圈,所以中间是必然会碰到慢指针的 - 而他走的圈数多少取决于X/M的比值,如果环很短,入环前很长,那么就会走很多很多圈,反之亦然
找到开始有环的位置(记录快慢指针相遇的位置,此时慢指针重回head,快慢指针保持相同步频前进,下次相遇的点就是环的起始点)
假设起点到环开始点距离为K,相遇点为环开始点后X,环的长度是M
此时慢指针总共走过 K + X
快指针总共走过 K + M * N(N为大于等于2的整数) + X
慢指针距离 * 2 = 快指针距离
2(K + X) = K + M * N +X
除项移项得到 K = M * N - X
由此可以推断从起点和初相遇点两边同时单步走K距离时,快指针恰好在入口处,因为M * N就是回到原地,-X就退回到了环起点
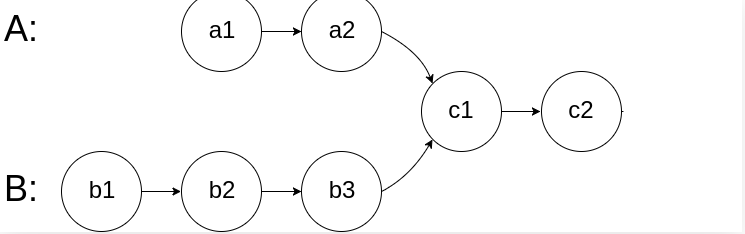
判断两个不等长的链表是否有相交(尾部相交,后面没有延伸)
- 核心就是怎么让AB两个指针同时达到C1
- 假设两个链表的长度为X和Y,相交的长度为M(>=0)
- A走X + (Y - M)步,走自身的长度,然后走B不想交部分的长度
- B走Y + (X - M)步
- 两者距离相等,且当M > 0时下一个节点必然是相交点,否则就是null节点
- 回到代码,就是AB节点同时从自己开始走,走完自己后,开始从对方的head走,然后必然会走到A === B的相遇节点,此时如果不是null的话,那就是相交了
队列
特点:先进先出 FIFO
主要技巧:
- 取模
在做循环队列时,比如10位的队列,在9的位置上添加新元素,那新元素会在0的位置上,如何得到就需要(9 + 1) % 10 = 0 。 同理,当第0位的元素,找上一个元素时,(0 - 1) % 10就会出现负数,此时可以(0 - 1 + 10) % 10 = 9得到正确的位置
栈
特点:后进先出
主要用途:
- 状态匹配,比如左右括号对称,tag封口
- 递归转迭代,比如二叉树的遍历用迭代来实现
二叉树
特点
- 每个节点度最大为2
- 即使只有一个子,也要区分是左子树还是右子树
性质
- 在二叉树的第i层,最多有2的
i-1次方的节点数 - 如果深度为k,那么最多有2的k次方减1个节点
- 度为0的节点数量比度为2的节点对一个
遍历
前中后序是遍历⼆叉树过程中处理每⼀个节点的三个特殊时间点
快速排序就是个⼆叉树的前序遍历,归并排序就是个⼆叉树的后序遍历
- 快排: 选一个数作为root,先遍历root,然后比root小的放进左子树,大的放进右子树。然后依次递归遍历左子树和右子树
- 归并:分割数组,一半为左子树,一半为右子树,先把左右子树遍历完,就得到了排好序的左右子树,此时最后回来遍历虚拟的root,把两边合并一下
⼆叉树题⽬的递归解法可以分两类思路,第⼀类是遍历⼀遍⼆叉树得出答案,第⼆类是通过分解问题计算出答案,这两类思路分别对应着 回溯算法核⼼框架 和 动态规划核⼼框架。
如计算二叉树的最大深度,两种方法
// 全遍历
// 记录最⼤深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;
// 主函数
int maxDepth(TreeNode root) {
traverse(root);
return res;
}
// ⼆叉树遍历框架
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
depth++;
if (root.left == null && root.right == null) {
// 到达叶⼦节点,更新最⼤深度
res = Math.max(res, depth);
}
traverse(root.left);
traverse(root.right);
// 后序位置
depth--;
}
// 分界问题,动态规划
const getDepth = (root) => {
if (!root) {
return 0;
}
return Math.max(getDepth(root.left), getDepth(root.right)) + 1;
};
前序位置的代码只能从函数参数中获取⽗节点传递来的数据,⽽后序位置的代码不仅可以获取参数数据,还可以获取到⼦树通过函数返回值传递回来的数据。所以在后续位置上可以做很多操作,⼀旦发现题⽬和⼦树有关,那⼤概率要给函数设置合理的定义和返回值,在后序位置写代码了。
如计算二叉树最大直径,在后序位置可以得到子树的最大值,
var diameterOfBinaryTree = function (root) {
let max = 0;
const findMaxDepth = (root) => {
if (!root) {
return 0;
}
const maxLeftSide = findMaxDepth(root.left);
const maxRightSide = findMaxDepth(root.right);
max = Math.max(maxLeftSide + maxRightSide, max);
return Math.max(maxLeftSide, maxRightSide) + 1;
};
findMaxDepth(root);
return max;
};
计算二叉树每层的最大值(用递归的方式做层序遍历)
var largestValues = function (root) {
const ans = [];
const traverse = (root, depth) => {
if (!root) {
return;
}
const max = ans[depth];
if (max === undefined) {
ans[depth] = root.val;
} else {
ans[depth] = Math.max(root.val, max);
}
traverse(root.left, depth + 1);
traverse(root.right, depth + 1);
};
traverse(root, 0);
return ans;
};
从前序与中序遍历序列构造二叉树
核心思想:
- 分割片段 - 确保两头的start/end是对应了同一颗子树
- 通过前序片段的第一位可以得到当前子树的root
- 通过root的值找到它在中序片段的位置index,此时index左边就是左子树,右边就是右子树
- 通过上一步得到的左子树知道左子树的节点个数size,这样
size + preStart就是左子树在前序的end - 以此类推,就得到了整个左右子树的范围
- 得到范围后,递归这个方法,构建左右子树。
var buildTree = function (preorder, inorder) {
const build = (preStart, preEnd, inStart, inEnd) => {
if (preStart > preEnd || inStart > inEnd) {
return null;
}
const rootValue = preorder[preStart];
const root = new TreeNode(rootValue);
const inRootIndex = inorder.indexOf(rootValue);
const preSize = inRootIndex - inStart;
root.left = build(
preStart + 1,
preStart + preSize,
inStart,
inRootIndex - 1
);
root.right = build(preStart + preSize + 1, preEnd, inRootIndex + 1, inEnd);
return root;
};
return build(0, preorder.length - 1, 0, inorder.length - 1);
};
搜索二叉树
搜索二叉树的特点是,任意节点的左子树所有点的值都比当前节点小,右子树的所有值都比当前值大。同时树里不应该有重复的数
最大的特性就是:中序遍历的结果是一个有序的数组
// 查找搜索二叉树
TreeNode searchBST(TreeNode root, int target) {
if (root == null) {
return null;
}
// 去左⼦树搜索
if (root.val > target) {
return searchBST(root.left, target);
}
// 去右⼦树搜索
if (root.val < target) {
return searchBST(root.right, target);
}
return root;
}
验证搜索二叉树的合法性
不仅仅要求根比左大比右小,更要看整颗子树的情况,所以要把最大最小值带下去
var isValidBST = function (root) {
const check = (node, min, max) => {
if (!node) {
return true;
}
// 注意都是加上等于这个条件,不然就会出现下面这种情况
// 3
// 1 2
// 0 3
if (min !== null && node.val <= min) {
return false;
}
if (max !== null && node.val >= max) {
return false;
}
// 相当于是个后序
// 检查左子树时,自己就是最大值,同时传下去上面的最小值
// 检查右子树时,自己就是最小值,同时传下去上面的最大值
return check(node.left, min, node.val) && check(node.right, node.val, max);
};
return check(root, null, null);
};
完全二叉树
完全二叉树 (complete binary tree):只有最后一层的右侧缺少节点的二叉树。这是一种特殊的结构,有几个神奇的特性
- 它可以在内存中连续存储,而不需要指针,从而节省空间。因为每层的数量最最后一层前都是固定的,所以可以直接按层从左到右存储,没有排满的就是最后一层
- 要得到完全二叉树的层数,只需要从根节点一直遍历左节点,即左沉底就能算出层数
- 知道任何节点的编号x,那么x * 2就是左节点的编号,x*2 + 1就是右节点的编号
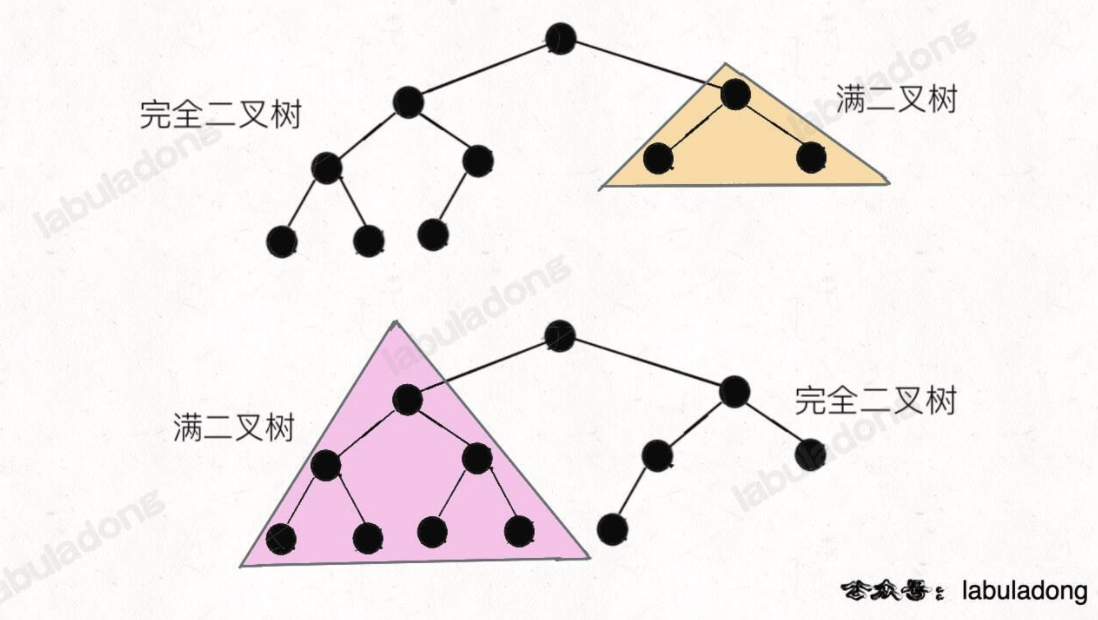
- 一棵完全二叉树的两棵子树,至少有一棵是满二叉树
- 如果要判断某个位置的节点是否存在,可以通过位置编号的二进制来计算 力扣222题
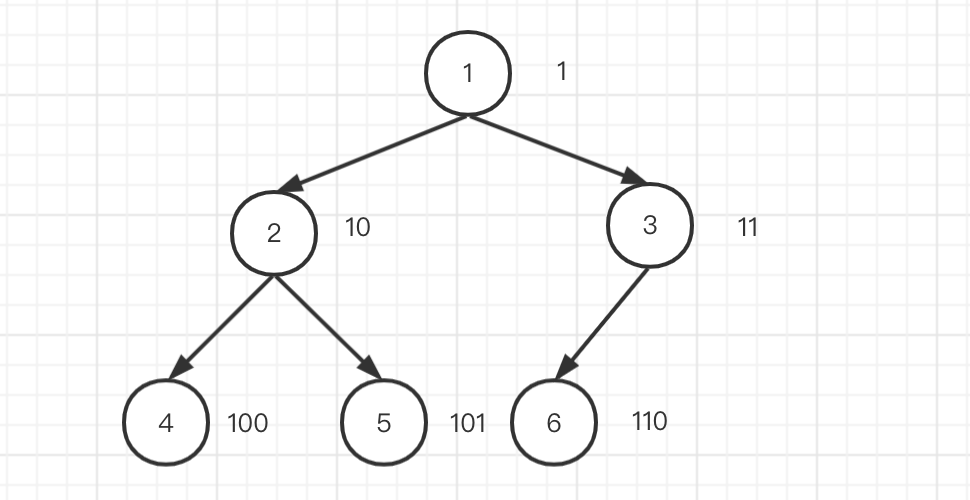
如图所示,将所有节点从1开始编号,从上到下,从左到右。同时将编号所对应的二进制标在旁边。发现有以下规律
- 所有编号的二进制都是1开头的,其实这是废话,只要不补位,那么肯定是1开头的,只是大家的位数不同
- 每层的标号位数和层数是一致的,第一层1位,第二层2位。。。
- 除了最后一层,每层的节点数是固定的2^(h-1),h为层数
- 最后一层的节点数量范围是[1, 2^(h-1)],这里就是1到4
- 最后一层节点的编号范围是[2^(h-1), 2^h - 1], 这里就是4到7
- 除了跟节点外,任意节点标号的二进制,抛开第一位,后面的位数依次就是从根节点到达此节点的路径,0就是左节点,1就是右节点
- 以5为例,标号101,从根节点开始0向左走一位,然后1向右走一位
- 这样的原因是:观察一下,10下面的节点,在增加一位的情况下,前两位永远也是10。同理11后面的节点也是11开头的
- 那么我们反推一下,101的上一层必然是10,10的上一层必然是1
取位技巧
如果当前已经知道5的二进制是101,那么如何可以取出0和1呢?
- 取任何三位二进制第二位,就可以通过和010与一下,如果结果是0那那位就是0,否则就是1。即101 & 010 = 010 不为零,即第二位为1。 相反如果是100 & 010 = 000则表示第二位为0
- 那么现在的问题就是怎么先得到10因子,这个值只能是10,100,1000. 如此例,层数是3,那么底层的二进制肯定是三位数的,所以是010,如果是4层那就是0100。得到规律这个数字就是1合上层数h-2个0,即
- 等到第二位取完之后,取第三位,就是把刚才得到的因子 x >> 1 右移一位即可
// 检查完全二叉树中,是否存在某顺序编号的节点
const exists = (root, level, k) => {
let bits = 1 << (level - 1); // 得到取位因子
let node = root;
while (node !== null && bits > 0) {
if (!(bits & k)) { // 如果因子与编号的结果是0,这应该从当前节点走左边节点遍历,相反走右边
node = node.left;
} else {
node = node.right;
}
bits >>= 1; // 因子右移一位
}
return node !== null;
};
// 具体实现在完全二叉树中,二分查找最后一个节点,从而得到总的节点数量
var countNodes = function (root) {
if (root === null) {
return 0;
}
let level = 0;
let node = root;
// 计算出层数
while (node.left !== null) {
level++;
node = node.left;
}
let low = 1 << level, // 计算出完全二叉树,在第N层的节点顺序范围
high = (1 << (level + 1)) - 1;
while (low < high) {
const mid = Math.floor((high - low + 1) / 2) + low;
if (exists(root, level, mid)) {
low = mid;
} else {
high = mid - 1;
}
}
return low;
};
递归流程
数学归纳法
- 首先k0是正确合理的
- 假设ki是正确的,那么k i+1应该也是正确的
- 则所有kn都是正确的
// fib(n) : 第n项斐波那契的值 function fib(n) { if(n <= 2) return n; // k0 // 假设fib(n - 1)正确,fib(n - 2)正确; // 则可以推出:fib(n) 一定是正确的 return fib(n - 1) + fib(n - 2); }明确函数的意义,比如这个函数的目的是遍历一个根节点
思考边界,比如为空就返回
实现
递归代码的精髓在于调用自己去解决规模更小的子问题,直到到达结束条件;而数学归纳法之所以有用,就在于不断把我们的猜测向上加一,扩大结论的规模,没有结束条件,从而把结论延伸到无穷无尽,也就完成了猜测正确性的证明。
比如做二叉树的层序遍历
- 根节点作为一个一位数组传入函数,是可以做到遍历的,同时通过遍历这个数组是可以得到所有第2层子节点的,表示k0可行,那么我们假设在第n层,我们可以传入第n层的所有节点,然后收集所有n+1层的节点,则整个递归关系是成立的
- 函数的意义是,传入一个节点数组,将数组的节点值都推入最终结果,同时将他们的所有子节点收集起来,再次传给自身函数。即
遍历节点数组,推入结果集,并收集下一层的节点数组,那么下一层节点数组的结果怎么呈现呢,就需要递归 - 边界即某一次函数执行结束后,没有收集到任何子节点,表示已经走到了最后一层
又比如计算一个二叉树的深度
- 明确函数:一个树的深度等于,
1 + 左子树的深度和右子树的深度的最大值,而左右子树的深度怎么来,就是需要递归 - 如果只有根节点,带入函数就是1
- 边界是节点不存在,就返回0
const getDepth = (root) => {
if (!root) {
return 0;
}
return Math.max(getDepth(root.left), getDepth(root.right)) + 1;
};
实现一维数组转树
const list = [
{ id: 1, pid: 0, name: '四川' },
{ id: 2, pid: 1, name: '成都' },
{ id: 3, pid: 1, name: '宜宾' },
{ id: 4, pid: 1, name: '绵阳' },
{ id: 5, pid: 1, name: '德阳' },
{ id: 6, pid: 2, name: '高新区' },
{ id: 7, pid: 2, name: '武侯区' },
{ id: 8, pid: 3, name: '翠屏区' }
];
const arrayToTree = (arr, pid) => {
return arr.reduce((res, current) => {
if (current['pid'] === pid) {
current.children = arrayToTree(arr, current['id']);
return res.concat(current);
}
return res;
}, []);
};
console.log(arrayToTree(list, 0))
堆
特性
堆结构其实就是一个完全二叉树
完全二叉树的好处是,可以在连续的内存空间(数组)里面直接描述树结构
完全二叉树,任意节点,知道自己的数组中的编号,得到父与子的编号,假设编号i (编号从0开始)
- 父节点的编号:
(i - 1) >> i, 这里i > 0, 如1的父为0,3的父为1 - 子节点的编号: 左节点
(i << 1) + 1,右节点(i << 1) + 2
- 父节点的编号:
分为大根堆和小根堆
大顶堆: 任意父节点都大于两个子节点
小顶堆:任意父节点都小于两个子节点
兄弟节点的大小关系是不明确的,只知道父子间的大小关系。所以最大(小)值永远是root,而第二大(小),可能在第二层,也可能在第三层
优先队列就是堆,就是原本先进先出的队列,变成了有优先级的,优先级高的先出
一般遇到找出最大K个元素之类的题目,且动态加一位,仍然要保持排序的, 一般都是要用堆排序
- 比如要求最大第K个元素,可以将初始化的数组,建立成一个小根堆
- 当堆长度大于K时,就循环pop,此时弹出的一定是比最大K元素小的元素
- 当堆长度等于K时,此K个元素就是所有元素中最大的K个, 此时堆顶元素就是,剩下K个元素中最小的,即所有元素中第K大的
- 此时如果push新元素进去,然后再pop一次,那么堆顶的依然是所有元素中第K大的
不要思维定式(373题)
- 求两个排好序的数组的两两组合,
和最小的前K个组合 - 此时就会思维定式想着建立小根堆,然后pop前K个元素,这样性能太差,因为是排序过的,只有前面的元素才有进堆的必要性
- 可以考虑建一个K位长度大根堆,此时push进去的元素如果小于堆顶元素,那么就是pop一个元素,push进去一个元素
- 否则说明当前push进去的数字,比当前最小的K的个数都大,所以可以直接略过,这样就跳过了堆排序的消耗
- 求两个排好序的数组的两两组合,
// 实现一个大根堆
class Heap {
constructor(values) {
this.data = values;
this.init();
}
size() {
return this.data.length;
}
init() {
for (let i = 0; i < this.size(); i++) {
this.bubbleUp(i);
}
}
swap(i, j) {
if (i === j) return;
const temp = this.data[i];
this.data[i] = this.data[j];
this.data[j] = temp;
}
bubbleUp(index) {
while (index > 0) {
const parentIndex = (index - 1) >> 1;
if (this.data[parentIndex] < this.data[index]) {
this.swap(index, parentIndex);
}
index = parentIndex;
}
}
pop() {
if (!this.size()) {
return null;
}
const top = this.data[0];
const last = this.data.pop();
if (this.size()) {
this.data[0] = last;
this.bubbleDown(0);
}
return top;
}
bubbleDown(index) {
while (index < this.size() - 1) {
const leftIndex = (index << 1) + 1;
const rightIndex = (index << 1) + 2;
let maxValIndex = index;
if (this.data[maxValIndex] < this.data[leftIndex]) {
maxValIndex = leftIndex;
}
if (this.data[maxValIndex] < this.data[rightIndex]) {
maxValIndex = rightIndex;
}
if (maxValIndex === index) break;
this.swap(index, maxValIndex);
index = maxValIndex;
}
}
push(val) {
this.data.push(val);
this.bubbleUp(this.size() - 1);
}
peek() {
if (this.size()) {
return this.data[0];
}
return null;
}
}
const heap = new Heap([99, 5, 12, 56, 1, 0, 8]);
const r1 = heap.pop(); // 99
const r2 = heap.pop(); // 56
heap.push(100);
const r3 = heap.pop(); // 100
实现核心
- 每插入一个数字,需要确保插入的这个数字是比父来的小,如果比父来得大,那就需要和父调换位置,分两种情况
- 在初始化数组时,每次不管是不是比父大,都要把index变成父index,做下一轮计算,直到顶层
- 在后续插入时,只要插入数小于父,那就直接停止
- 每pop一个数字,这个数字就是目前的最大值,此时要做的事情是
- 把队尾的数字,放到队首来,填补pop后的空缺
- 自顶向下,比较子与父的值
- 如果子大于父,那么就要调换位置,然后小的数字来到子的位置充当父,继续父子值的比较
- 如果子都小于父,那么说明目前结构正确,直接跳出循环
回溯
回溯主要用在数字的全排列或者例举出所有可能性的问题上。回溯的本质就是暴力穷举
列出所有可能性其实就是所有可选类型的排列组合,当选择A为第一个选项后,选项数-1,已选项+1。 剩下的选项重复重复这个步骤。
// 排列组合的公式
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
回溯的应用无外乎三种场景:排列,子集,组合
排列
46题全排列
本质上就是深度遍历一棵决策树
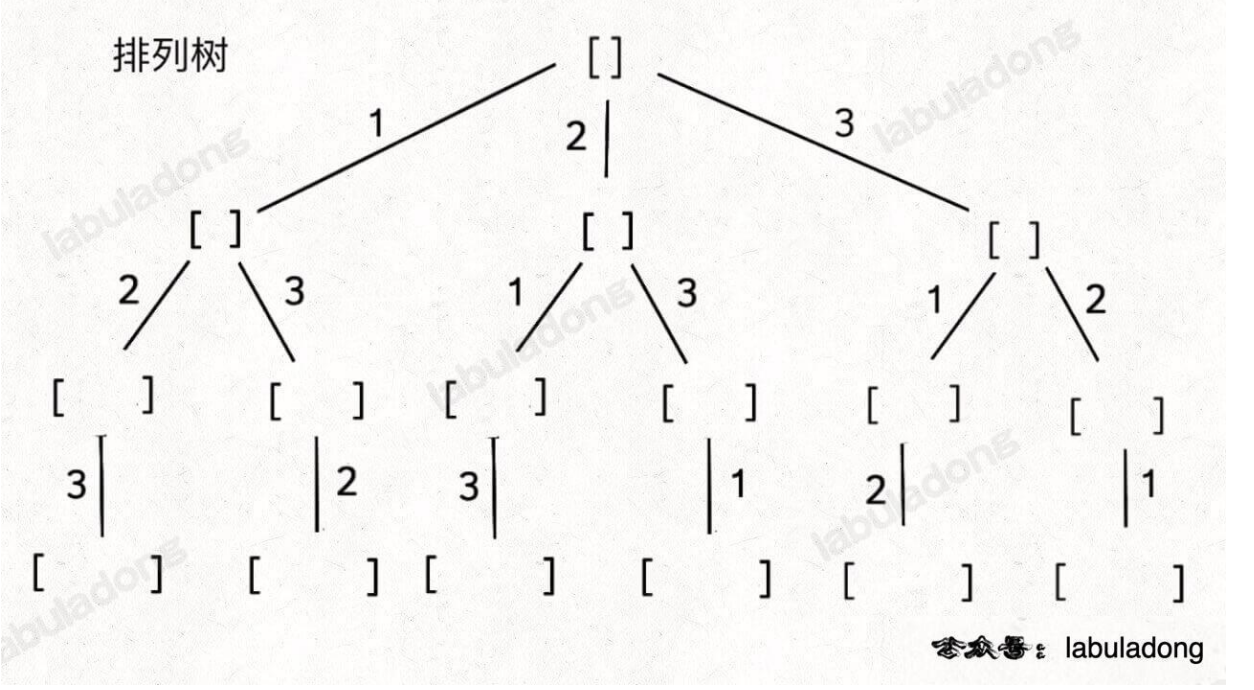
考虑三个元素
- 路径:也就是已经选择了的节点,我们称之为
track - 可选列表:表示当前可以选择的节点列表,成为
opts - 结束条件:什么时候到底结束的条件
具体过程:
- 定义两个变量,result存放最终结果,track存放路径
- 在开头定义结束条件,这里的条件是当opts为空的时候表示到底了,然后return,不要继续下面的递归了
- 从根开始,opts是全量, 遍历第一个子节点,加入track,同时开始递归,把opts中的第当前节点filter掉
- 未触发结束条件,则继续第三步,直到消耗掉opts能满足结束条件
- 满足结束条件表示,在当前的选择下,后面的选择都已经穷举完了
- 比如说track中只有1,当递归完成时,说明当第一位是1这个路径时,后面的路径[2, 3]/[3, 2] 都已经排好了
- 即说明1占据这个位置的所有可能性都已经举完了
- 所以1就可以退位,让给后面的元素进来,所以要pop它
- 注意最后在结束条件添加result的时候,要给track做一个浅拷贝,不然最终的结果就都一样了
// 全排列
const result = [];
const track = [];
const backTrack = (opts) => {
if (!opts.length) {
result.push([...track]); //
return;
}
for (let i = 0; i < opts.length; i++) {
track.push(opts[i]);
backTrack(opts.filter(_opt => _opt !== opts[i]));
track.pop();
}
};
backTrack(nums);
return result;
子集
与全排列基本类似,区别在于子集的元素顺序是固定的,所以只需要简单调整下
- 全排列传入的是剩下可选的opts
- 子集传入的是接下来的index,index只能一路加加,所以就不会出现重复的元素,相当于变相限制这个opts只能是后面的元素
var subsets = function (nums) {
const ans = [];
const track = [];
const backtrack = (startIndex) => {
ans.push([...track]);
for (let i = startIndex; i < nums.length; i++) {
const cur = nums[i];
track.push(cur)
backtrack(i + 1);
track.pop();
}
};
backtrack(0);
return ans;
};
组合
77题组合
其实就是延续前面两种情况,区别是在结束条件上做一些限制
var combine = function (n, k) {
const ans = [];
const track = [];
const backtrack = (startIndex) => {
if (track.length === k) {
ans.push([...track]);
return;
}
for (let i = startIndex; i <= n; i++) {
track.push(i);
backtrack(i + 1);
track.pop();
}
};
backtrack(1);
return ans;
};
复杂例子
93题,复原IP地址
也是在上面的基础上做变形
var restoreIpAddresses = function (s) {
const result = [];
const track = [];
const backTrack = (startIndex) => {
if (track.length === 4) {
if (startIndex === s.length) {
result.push(track.join("."));
}
return;
}
for (let i = startIndex; i < s.length; i++) {
let _temp = s[i];
while (+_temp >= 0 && +_temp <= 255) {
track.push(+_temp);
backTrack(i + 1);
if (+_temp === 0) {
track.pop();
break;
}
i++;
_temp = _temp + s[i];
track.pop();
}
break;
}
};
backTrack(0);
return result;
};
动态规划
总体思想就是把大的问题化解成小的子问题。最简单的比如斐波那契,求第N个数字,其实就是N-1和N-2两个数字的和。那么这就会被分界为直到1的N个子斐波那契数的问题。
经典的找零问题,有三种货币面额分别是[1, 5, 11],给定总数面值n,问所需最少货币数凑出n
得到一个方程: f(n) = Math.min((f(n - 1) + 1), (f(n-2) + 1), (f(n-5) + 1))
即我假设我确定最后付出一个面额是x,那么在这个前提下,只要求出凑n-x 这个总额的最优解然后加一就好了,这就可以和斐波那契一样递归解决了,代码大致如下
function f(n) {
if(n === 0) return 0
let min = Infinity
if (n >= 1) {
min = Math.min(f(n-1) + 1, min)
}
if (n >= 5) {
min = Math.min(f(n-5) + 1, min)
}
if (n >= 11) {
min = Math.min(f(n-11) + 1, min)
}
return min
}
console.log(f(15)) // 3
但这样会有两个问题,
- 如果n非常大,直接这么计算会重复计算非常多次相同的子问题,解决方法可以是加一个缓存来记录
- 递归最大的问题就是会有爆栈的风险,如果n超过20000就随时会爆
所以另外一种方式就是转递归为迭代,递归的思想就是不要从顶向下而是自底向上,因为我们知道,这种递归的结束条件就是n到0,即从0到n的所有中间结果其实都是要计算的,那不如直接从0开始一个个向上计算
以上是比较简单的一维动态规划,一般还有更加复杂的范围动态规划,比如最长回文子序列 ,求一个字符串s中最长的回文子序列(可以删除字符)长度。
我们假设最长的子序列开始和结束的下标分别为low和high,这些下标可能是字符串中的任意位置
此时我们建立一个二维数组dp[low][high],来记录所有的可能性,即所有子问题的可能结果
- 假设low和hight相同,即长度只有1,所以结果也是1
s[low]和s[high]相同,那么low和high肯定是可以形成回文的,那只要求出dp[low+1][high-1](这个表示两个下标间最大的可能性)然后+2即可s[low]和s[high]不相同,表示头尾是不可能形成回文的,这里就要求出Math.max(dp[low][high - 1], dp[low + 1][high]),表示头或者尾不变的前提下,对方缩进一位的最大值- 最后只要取出
dp[0][s.lengt-1]即可 - 要注意遍历顺序,low不能从0开始,必须从最大值开始,数据才能准备好。因为在一个二维矩阵中,求一个值就等于当前左边和下边两个值的和。 左边就是
[low][high - 1]下边就是[low + 1][hight],比如下面要计算dp[3][4],需要的就是dp[3][3]和dp[4][4],这时候数据已经准备好了。

BFS
BFS的最常见使用场景,就是寻找最短路径,时间复杂度会比DFS强很多
二叉树的层序遍历其实就是BFS的一个具体实现。大致框架就是
- 准备一个队列,注意是队列,要先进先出,所以要用shift配合push
- 以一层为单位,做一轮遍历,遍历完了也就push完了下一层的元素
- 期间加入终止条件
// 二叉树最小深度
var minDepth = function (root) {
if (!root) {
return 0;
}
const queue = [root];
let depth = 1;
while (queue.length) {
const size = queue.length;
for (let i = 0; i < size; i++) {
const cur = queue.shift();
if (!cur.left && !cur.right) {
return depth;
}
cur.left && queue.push(cur.left);
cur.right && queue.push(cur.right);
}
depth++;
}
return depth;
};
通用技巧
因为js里面0直接去判断非空会为false,所以有的时候0为有意义的值的时候,比如记录指针下标,最后要判断下标是不是为空。如果这时候把空指针用null来指定,那接下来所有的判断都要加上x !== null 非常不方便,可以将下标设置为-1,然后判断是不是大于等于0就好
遇到字符串计数相关的问题,可以考虑用Map来做count计数
逆向思维
比如合并排序的数组这题,表面上是要从前到后合并排序,如果这么做的话就要涉及数组的移位,计算空值等问题。如果换个思路,从尾巴上开始,从两个数组中取出最大的放在最后的位置。这样就规避了上面的问题且要考虑的边界问题就少很多。
var merge = function (nums1, m, nums2, n) {
let x = m - 1;
let y = n - 1;
for (let i = m + n - 1; i >= 0; i--) {
let max;
if (x < 0) {
nums1[i] = nums2[y--];
continue;
}
if (y < 0) {
nums1[i] = nums1[x--];
continue;
}
if (nums1[x] > nums2[y]) {
max = nums1[x];
x--;
} else {
max = nums2[y];
y--;
}
nums1[i] = max;
}
};
比如各种动态规划问题,比如背包,N的体积如何价值最大化。如果正向从0开始凑,就会发现后面的问题无比复杂,还不如从尾开始,确定最后一个要放进去的是什么,比如M,然后问题就变成了(N - M)下的背包问题,如果就变成了一个可以递归的子问题。加上缓存之后,就能高效得解出问题
前缀技巧
前缀和主要适⽤的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。

var NumArray = function(nums) {
this.preSum = new Array(nums.length + 1).fill(0);
for (let i = 1; i <= nums.length; i++) {
const element = +nums[i-1];
this.preSum[i] = this.preSum[i-1] + element;
}
};
NumArray.prototype.sumRange = function(left, right) {
return this.preSum[right + 1] - this.preSum[left];
};
通过在初始化时,计算出每个元素他之前所有元素的和并存起来,当求ab之前的和时,就等于b的后一位的sum减去a前一位的所有sum。这就非常高效。 同理可以应用到矩阵中去(304题)
重要核心: preSum需要留空一位,preSum[i]表示从0到i-1位的总和。为什么要留一位?是为了当题目要算sumRange(0,0)这样的case时,不会越界,表示下标0的前一位sum就是0
同理304题,矩阵区间求和
var NumMatrix = function (matrix) {
// preSum[x][y]表示 [0,0] 到 [x-1,y-1]的总和
const m = matrix.length;
const n = matrix[0].length;
const preSum = new Array(m + 1);
for (let i = 0; i < m + 1; i++) {
preSum[i] = new Array(n + 1).fill(0);
}
for (let i = 1; i < m + 1; i++) {
for (let j = 1; j < n + 1; j++) {
preSum[i][j] =
preSum[i - 1][j] +
preSum[i][j - 1] +
matrix[i - 1][j - 1] -
preSum[i - 1][j - 1];
}
}
this.preSum = preSum;
};
NumMatrix.prototype.sumRegion = function (row1, col1, row2, col2) {
return (
this.preSum[row2 + 1][col2 + 1] -
this.preSum[row1][col2 + 1] -
this.preSum[row2 + 1][col1] +
this.preSum[row1][col1]
);
};
有序特征
很多题目都有数组或者链表已经有序的特征,然后比如要去重,这时候即使忽略这个特征最终也是可以做出答案的,但是就丧失了一种优雅的解法。此时会发现在有序的情况下重复的数字一定是挨在一起的。所以可以用快慢指针来处理问题
- 快指针探路。如果快指针和慢指针的值不同,那么慢指针可以+1,然后把快指针的值赋值给慢指针
- 否则快指针继续向前,直到队尾
- 计算各种字符串子串(不是子序列)都要优先考虑滑动窗口法,因为子串是连续的,理论上滑动肯定能找到最终解的(第3/76题)
- 滑动窗口的核心就是双指针,fast一直向右滑,直到满足条件停下来,然后low向右滑,直到不满足条件停止,此时得到的肯定是一个符合答案的相对解
- 然后fast继续右滑,循环上一步,直到fast到了尾巴。每次左指针停止的时候计算下是否最优解
- 可能需要两个Map来记录值,一个是窗口中存在的值,一个是必须满足的值,两者用来做比对,看是否满足需求
快速swap
- 很酷的swap,但仅限于数字内容
const swap = (i, j) => { // 假设 i j 内容为1和2
nums1[i] ^= nums2[j]; // nums1[i] = 3
nums2[j] ^= nums1[i]; // nums[j] = 1
nums1[i] ^= nums2[j]; // nums[i] = 2
};
- 更实用的swap
const swap = (array, a, b) => [ array[ b ], array[ a ] ] = [ array[ a ], array[ b ] ]
原地修改
经常会有题目要求是原地修改,比如27题移动元素,要求移除指定元素,此时可以使用快慢指针,如果元素不等于目标,则快慢指针一起前进,否则慢指针不动,快指针前进
// 原地删除数组中的undefined
slow = 0
fast = 0
while (fast < chars.length) {
if (chars[fast] !== undefined) {
chars[slow] = chars[fast];
slow++;
}
fast++;
}
发散的双指针
典型用法就是寻找最长的回文子串
String longestPalindrome(String s) {
String res = "";
for (int i = 0; i < s.length(); i++) {
// 以 s[i] 为中⼼的最⻓回⽂⼦串
String s1 = palindrome(s, i, i);
// 以 s[i] 和 s[i+1] 为中⼼的最⻓回⽂⼦串
String s2 = palindrome(s, i, i + 1);
// res = longest(res, s1, s2)
res = res.length() > s1.length() ? res : s1;
res = res.length() > s2.length() ? res : s2;
}
return res;
}
单调栈
单调栈就是一个有序的栈,递增或者递减。用来处理一些特定的问题,比如下一个更大的数(496),给定一个数组,找出每一位接下来比他自己大的数,并放在它的位子上。比如下面的例子,它就是一个递减的数组
核心思想:
- 维护一个栈,里面存放比当前点值大的数,因为是push进去的,所以靠近栈顶的就离当前点最近
- 从数组的尾巴开始遍历,看栈是否为空
- 空的话,表示后面没有比当前大的数,返回-1
- 不空,从栈尾取数,如果比当前小,那就说明比当前更大的还在后面,这位没用了直接pop出去,直到找到比当前值大的数或者栈为空
- 此时栈顶的元素就是下一个比当前大的数
var nextGreaterElement = function (nums1, nums2) {
const map = {};
const stack = [];
for (let i = nums2.length - 1; i >= 0; i--) {
const cur = nums2[i];
while (stack.length && stack[stack.length - 1] < cur) {
stack.pop();
}
map[cur] = !stack.length ? -1 : stack[stack.length - 1];
stack.push(cur);
}
const ans = [];
for (let i = 0; i < nums1.length; i++) {
const cur = nums1[i];
ans.push(map[cur]);
}
return ans;
};
除此之外,栈除了可以存值,还可以存下标,比如每日温度(739),通过记录下标,可以知道两个值之间相距的距离
例题
对象的层序遍历
const obj = {
a: {
b: {
c: { f: 'aa' },
},
d: {
e: { g: 'bb' },
h: { i: 'cc' },
},
j: {
k: 'dd',
},
},
};
const result = [];
const getKeys = (stack) => {
if (!stack.length) {
return;
}
for (let i = stack.length - 1; i >= 0; i--) {
result.unshift(Object.keys(stack[i])[0]);
}
const tempStack = [];
while (stack.length) {
const cur = stack.shift();
const curKey = Object.keys(cur)[0];
if (!cur[curKey] || typeof cur[curKey] === 'string') {
continue;
}
const subKeys = Object.keys(cur[curKey]);
for (const key of subKeys) {
tempStack.push({ [key]: cur[curKey][key] });
}
}
getKeys(tempStack);
};
getKeys([obj]);
console.log('result: ', result);
// 输出 [f,g,i,c,e,h,k,b,d,j,a]
求二叉树公共父节点
思路:
- 只有两种可能的情况,第一种,两个点互为父子链路上的节点
- 两个点分别在某个点的两侧,不可能有第三种情况
- 当自身等于p或者q,且左右子任一找到另一个值,得到答案
- 但左右子同时找到目标值,此时自身也是答案
var lowestCommonAncestor = function (root, p, q) {
let ans;
const dfs = (root, p, q) => {
if (root === null) return false;
const lson = dfs(root.left, p, q);
const rson = dfs(root.right, p, q);
if (
(lson && rson) ||
((root.val === p.val || root.val === q.val) && (lson || rson))
) {
ans = root;
}
return lson || rson || root.val === p.val || root.val === q.val;
};
dfs(root, p, q);
return ans;
};
给一个数字比如1234,求出当前数字随意排列后,比当前数字大,但是是所有比当前数字大的组合中最小的
比如给出1234, 答案就是1243 解释: 比如4321肯定比1234大,但是肯定不是那个最小的。 1243就是所有排列组合里面比1234大,但又是所有比它大的数字里最小的
const param = 51342;
const findNextMax = (target) => {
const nums = `${target}`.split("").map(Number);
const possibleAns = [];
for (let i = nums.length - 1; i >= 0; i--) {
const cur = nums[i];
for (let j = i - 1; j >= 0; j--) {
const next = nums[j];
if (cur > next) {
const temp = [...nums];
[temp[i], temp[j]] = [temp[j], temp[i]];
possibleAns.push(+temp.join(""));
}
}
}
return possibleAns.length ? Math.min(...possibleAns) : null;
};
const result = findNextMax(param);
console.log("result: ", result);
思路:
- 肯定要从尾巴动手,这样才能找得到最小的
- 找到尾巴上的数,然后找到比它小的里面位置最接近的,然后交换,肯定结果是后者大。但是不能保证是最小的那个,比如51342结果就是52341,显然这是不对的,51432才是更优解。这个思路只能求出,确定要移动当前这个数字的情况下的最优解
- 所以这个方案是不全面的,我们只能一位位递推,每前进一位,求出确定移动当前位的情况下,能得到的最优解。也就是说我们得到了每个数字被移动得到的最优解,最后从中求一个最小值即可
- 每个数字只要考虑自己前面的数字比较即可,后面的已经被后面的数字考虑过了